Построение обученной нейросети
Пусть перед нами экран, разбитый на двенадцать клеток, 4?3. Клетки отображают дискретность элементов изображения. При фокусировании изображения клетка либо засвечивается, либо нет. "Засветка" определяет единичное значение величины ее возбуждения, "не засветка" - нулевое. Так, буква О
определяет засветку клеток, определяемую на рис. 2.1. Буква А засвечивает экран, как показано на рис. 2.2.

Рис. 2.1. Обучение букве "О"

Рис. 2.2. Обучение букве "А"
Что надо сделать для распознавания этих двух букв? Для того, чтобы некий конструируемый нами прибор мог сказать, какая это буква?
Очевидно, надо все сигналы возбуждения клеток экрана, засвечиваемой буквой О, подать на конъюнктор, реализующий схему И. Единичный сигнал на выходе конъюнктора, как показано на рис. 2.1, сформируется тогда и только тогда, когда засветятся все клетки экрана, на которое ложится изображение буквы О. Наличие единичного сигнала на выходе конъюнктора и определит ответ "Это буква О".
То же необходимо сделать и для буквы А.
Пометим каждую клетку экрана ее координатами. Тогда на языке математической логики сделанное нами можно записать в виде логических высказываний - предикатов:
(1,2)






(1,2)








Эти предикаты определяют "электронное" воплощение методами схемотехники.
При этом буквы не будут "мешать" друг другу, так как засветка соответствующих им клеток экрана частично не совпадает и единичное значение конъюнкции определится только для одной из них.
А если на экран подать букву К? Тогда ни один из двух конъюнкторов не выработает единичное значение, так как не произойдет полное совпадение засветки соответствующих им клеток экрана. Чтобы "научить" систему букве К, необходимо ввести еще один конъюнктор и проделать те же построения, что и выше.
Таким образом, мы можем говорить, что построили систему распознавания двух "правильно" заданных букв.
Но что делать, если буквы на экране пишутся дрожащей рукой? Тогда мы должны разрешить альтернативную засветку каких-то соседних клеток экрана и учитывать это с помощью операции дизъюнкции, ИЛИ. Как известно, в результате выполнения этой операции формируется единичный сигнал в том случае, если на входе есть хоть один единичный сигнал.
Рассмотрим возможность распознавания буквы О, допустив возможность засветки клеток (1,1), (1,3), (4,1), (4,3). Тогда ранее построенный предикат примет вид
((1,1)










Аналогично, для буквы А допустим засветку клеток (1,1) и (1,3):
((1,1)










Объединив оба предиката, получим схему на рис. 2.3.
Таким образом, мы реализовали для обучения и распознавания "схемотехнический" подход, основанный на применении булевых функций и оперирующий булевыми переменными 0, 1.
Теперь совершим тот шаг, тот переход, который и определяет гениальную простоту природного воплощения, рассчитанного на неполноту данных, недостоверность, "зашумленность", высокое быстродействие, надежность и унифицированность. Ибо мы не можем представить себе электронную схему, укрытую в черепной коробке.
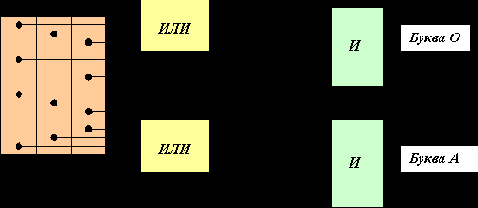
Рис. 2.3. Совместное обучение буквам "О" и "А"
Природа (и мы, как ее часть) никогда не располагает точной, определенной и достоверной информацией. Засветка клеток экрана, как и рецепторов нашего глаза, не бывает полной, образ не бывает правильным, присутствуют шумы, пропуски и т.д. Тогда жизненную важность обретают понятия похожести, ассоциаций. "На что более всего похож "показанный" образ, возникшая ситуация, и какие ответные действия наиболее обоснованы?" - вот вопрос, определяющий принцип нашей жизни среди многих опасностей и свершений. Ассоциативность нашего мышления является абсолютной.
Значит, надо уйти от вполне определенных булевых переменных (0, 1, "да - нет", "белое - черное" и т.д.) в сторону неопределенности, достоверности или других оценок информации, - в сторону действительных переменных.
Но тогда необходимо уйти и от булевой алгебры, так как понятия конъюнкции и дизъюнкции для действительных переменных не определены.
Тут и приходит на помощь анализ и применение принципов природной реализации - принципов нейронной сети, воплощенных в нашем мозге.
Преобразуем полученную нами обученную схему в нейронную сеть (рис. 2.4).
Каждая клетка экрана - это нейрон-рецептор, который в результате засветки обретает некоторую величину возбуждения, принимающую значение между нулем и единицей. Рецепторы, заменившие экран, образуют входной, или рецепторный, слой нейросети. Каждый конъюнктор и дизъюнктор заменим единой для всей сети моделью нейрона. Введем выходной слой сети, состоящий в нашем примере из двух нейронов, возбуждение которых определяет результат распознавания. Назовем нейроны выходного слоя по названиям букв - О и А.
Рецепторы, подобно экрану, возбуждаются извне. Все же другие нейроны, имитируя распространение возбуждения в мозге, реализуют передаточную функцию. Она преобразует сигналы на входе нейрона, с учетом весов этих входов (пока отложим их рассмотрение), в величину возбуждения данного нейрона, передаваемого далее по сети в соответствии со связями нейронов и достигающего выходного слоя.
Поскольку работа мозга имитируется на логическом уровне, передаточная функция выбирается достаточно простой. Так, в нашем примере достаточно выбрать следующую передаточную функцию для нахождения величины возбуждения i-го нейрона:


Рис. 2.4. Нейронная сеть для распознавания букв "О" и "А"
Здесь суммируются все сигналы (величины возбуждения), которые пришли от нейронов, связанных с данным. Порог может быть единым для всех нейронов.
Проверим, как построенная нейросеть реагирует на четко заданные эталоны букв. Под четкостью будем понимать то, что величина возбуждения, реально отражающая достоверность, максимальна и равна единице. Пусть при показе буквы О засветились нейроны-рецепторы (1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 3), (4, 2).
Тогда, при h = 0 величины возбуждения нейронов примут значения V1 = 3 , V2 = 1 , VO = 8 , VA = 7 . Нейрон О
возбудился более, чем нейрон А, указывая тем самым, что скорее всего была показана буква О. Аналогично можно рассчитать реакцию нейросети на все возможные конфигурации четко заданных эталонов букв.
А теперь введем ту самую неопределенность, к которой мы так стремились. Пусть в процессе показа буквы О четкость утрачена и величины возбуждения нейронов-рецепторов принимают значения V(1,1) = 0,2 , V(1,2) = 0,7 , V(1,3) = 0 , V(2,1)
= 0,5 , V(2,2) =0,1 , V(2,3) = 0,5 , V(3,1) = 0,5 , V(3,2) = 0,5 , V(3,3) = 0,1 , V(4,1) = 0,4 , V(4,2) = 0,4 , V(4,3) = 0,5 . Считаем: V1
= 0,9 , V2 = 1,3 , VO = 3,8 , VA = 3,9 .
Что ж, по-видимому, мы потребовали невозможного. Ведь при таком "крупнозернистом" экране налагаемые на него образы букв О и А пересекаются весьма существенно, и зашумленный показ букв обладает малой устойчивостью.
Рассмотренный принцип распознавания является обобщением принципа простейшего Персептрона, предложенного Ф. Розенблатом в 1959 г. [4] и ставшего классическим.
