Устойчивость, помехозащищенность и локализация максимального возбуждения
"…Цинциннат брал себя в руки и, прижав к груди, относил в безопасное место".
В. Набоков. "Приглашение на казнь"
На рассмотренном маленьком примере, где мы предположили жесткое закрепление нейронов выходного слоя между образами, принцип ассоциации "на что более всего это похоже" пока не виден. Как же он появляется?
Уместны ассоциации, предположения о том, как это реализовано в природе.
Представим себе отдельно выходной слой (рис. 2.17).
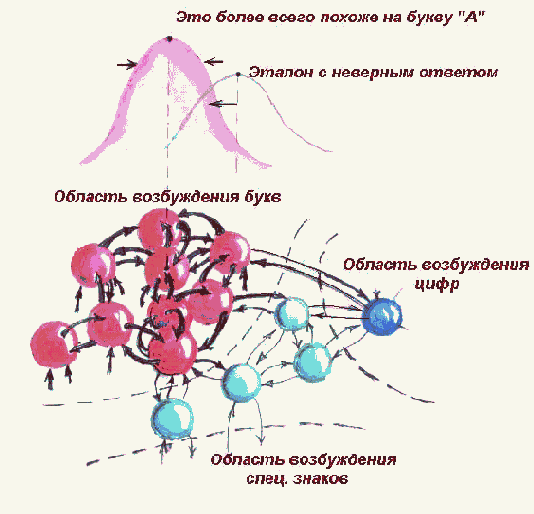
Рис. 2.17. Области возбуждения
Рассматривая прохождение возбуждения, например, при подаче того же изображения буквы А, в модели нейросети, ближе к реальному мы можем предположить, что не один нейрон, строго соответствующий этой букве, придет в возбужденное состояние, как это предполагается в логической модели, в его окрестности возбудятся и другие нейроны. Эта величина возбуждения будет угасать с ростом удаления. Нам же будет нужно, чтобы максимальной величиной возбуждения в этой окрестности обладал именно отмеченный нейрон. Более того, желательно, чтобы этот и только этот нейрон обладал высокой, существенно различимой величиной возбуждения. Это обеспечит определенность и однозначность при дальнейшем использовании полученного вывода для принятия решения и для построения других логических цепочек, использующих это решение. Такая локализация сигнала возбуждения позволяет ответить на вопрос: "на что более всего похож предъявляемый образ, несмотря на случайные отличия и оказываемые помехи?"
Кстати, такое предположение указывает на другое, фактически реализуемое предположение о непрерывности перерастания свойства похожести одних образов в другие. Следование этому принципу при принудительном закреплении нейронов выходного слоя способствует построению адекватных моделей. А точнее, подавая первый раз букву А, не следует указывать системе, какой нейрон выходного слоя должен возбудиться. Лучше подать достаточно "правильный" эталон и посмотреть, какой нейрон возбудится. Этот нейрон и будет впредь соответствовать нашей букве.
Возбуждения именно этого нейрона мы будем добиваться при предъявлении других эталонов.
(Хотя, мы же далее предполагаем, на основе уже рассмотренных примеров, что первоначально сеть "пуста", т.е. все веса - нулевые. Путь же возбуждения прокладывается, "трассируется".)
Способы максимизации и локализации уровня возбуждения основаны на нахождении экстремума функции возбуждения, построенной на области выходного слоя. Здесь нельзя обойтись без обмена тормозящими воздействиями между нейронами выходного слоя. Простейшая идея состоит в следующем. Все нейроны области выходного слоя имеют между собой синапсические связи, так что каждый нейрон связан с ближайшими нейронами тормозящими связями, по модулю пропорциональными величине собственного возбуждения. Тогда в итоге взаимодействия двух нейронов (один из алгоритмов такого взаимодействия нейронов выходного слоя будет рассмотрен) более "сильный" нейрон сохранит положительный (хотя и меньший) потенциал, сообщив более "слабому" нейрону тормозящее воздействие. Такое пошаговое "голосование" на фоне приходящего подтверждения от эталона и выделит сильнейшего.
Итак, мы видим, что обучение сети неразрывно связано с локализацией возбуждения на выходном слое.
Анализируя все сказанное выше, мы можем попытаться собрать некоторую универсальную модель нейросети. В ней будут присутствовать входной и выходной слои. Картина возбуждений выходного слоя при подаче изображения на входной слой будет представлять собой (после аппроксимации в непрерывную область определения из дискретной) непрерывную функцию, максимум которой должен определить нам необходимое заключение. Однако на этапе обучения (да и в рабочем режиме - с удовлетворяющей нас достаточно малой вероятностью) по ряду предъявляемых эталонов этот максимум не совпадает с желаемым ответом. Следовательно, путь распространения возбуждений внутри сети необходимо скорректировать изменением синапсических весов нейронов, оказавшихся задействованными в этом процессе.
Было сказано, что предварительная локализация максимума величины сигнала производится в результате взаимодействия нейронов в области или некоторой окрестности выходного слоя или коры. Получается так, что области возбуждений оказываются "закрепленными" за типами объектов - за буквами, цифрами, продуктами питания и т.д. В развитой сети, где становится актуальным понятие коры, нейроны отдельных ее областей через нейроны внутренних слоев вновь порождают пути прохождения возбуждений в другие области коры и т.д.
Пытаясь разгадать и воспроизвести универсальную нейросеть, мы вновь и вновь пытаемся "заглянуть в зеркало". Мы видим, что хотя отдельный нейрон обладает возможностями взаимодействия с огромным числом нейронов (нейрон имеет до 10 тысяч дендритов), это взаимодействие характеризуется локальностью. А именно, несмотря на случайность связей, вероятность связи с "близким" нейроном значительно выше вероятности связи с нейроном "далеким". Об этом говорят даже исследованные длины дендритов и аксонов. (Длина дендрита достигает одного миллиметра; однако длина аксона достигает сотен миллиметров. При этом применяется, по-видимому, усредненная характеристика, вряд ли принимающая во внимание нейроны только лишь головного мозга.)
Такой принцип локальности, пронизывающий всю структуру сети, в сочетании с принципом иерархии - возможностью построения новых выводов на основе сделанных - позволяет на деле реализовать связи "каждый с каждым". Никакой вывод не может оставаться недоступным и неиспользованным при построении сложных умозаключений.
Принцип локальности обеспечивает минимизацию входной информации, существенное влияние лишь значимых признаков на заключение, контролируемое и диагностируемое по функциональное разбиение областей нейросети, определение и выделение той области нейросети, в синапсические веса которой необходимо внести поправки в процессе обучения (например, организовать прилив крови).
Принцип локальности не отвергает существования маловероятных связей "каждый с каждым".
Эта вероятность может быть высокой вследствие аномалий генетического характера. Например, человек, которого мы относим к уникумам, может видеть кожей вследствие того, что нейроны, воспринимающие кожные ощущения, сильно связаны с нейронами выходного слоя, "отвечающими" за зрение. И вместо того чтобы возбуждение в сторону последних при слабых связях угасло, оно становится результативным. Ведь в целом все нейроны устроены одинаково!
Большое число связей способствует высокой надежности мозга. Ведь ежедневная гибель огромного числа нейронов, подхлестанная алкоголем и наркотиками, а также травмы, компенсируются другими путями прохождения возбуждений, иногда даже связанными с необходимостью переобучения. Впрочем, ограниченный ресурс возможного не спасает, в конце концов, от деградации.
Итак, рассмотрим более подробно процесс локализации максимальной величины возбуждения на выходном слое, заключающейся в выделении того нейрона некоторой малой области, величина возбуждения которого максимальна. Он основан на подавлении тех сигналов возбуждения нейронов, которые не соответствуют нейрону с максимальным возбуждением. Т.е. если необходимо сконцентрировать сигнал и выделить нейрон с максимальной величиной возбуждения, это достигается с помощью подавляющих связей, с которыми действуют друг на друга "соседние" нейроны выходного слоя.
Пусть в целом над нейронами выходного слоя, условно расположенного на плоскости (x, y), можно построить непрерывную функцию их возбуждения P(x, y) (рис. 2.18), обусловленную прохождением сигналов возбуждений в сети на основе предъявленного эталона. Будем считать, что эта функция имеет один или более максимумов. Пусть Pij
- значение величины возбуждения нейрона с координатами (i, j).
Каждый нейрон (i, j), действуя в своей окрестности, рассылает соседним нейронам, на их дендриты с отрицательными, не обязательно регулируемыми, весами, свою величину возбуждения Pij, первоначально полученную из сети.
Представим взаимодействие двух "близких" нейронов, например (i, j) и (i, j+1), получивших первоначально разные значения величин возбуждения из сети.
Пусть Pij > Pi,j+1
. Тогда в очередном такте времени на входе нейрона (i, j) появится подавляющий сигнал Pi,j+1
, а на входе нейрона (i, j+1), и так имеющего меньшее значение величины возбуждения, - подавляющий, больший сигнал Pij
.
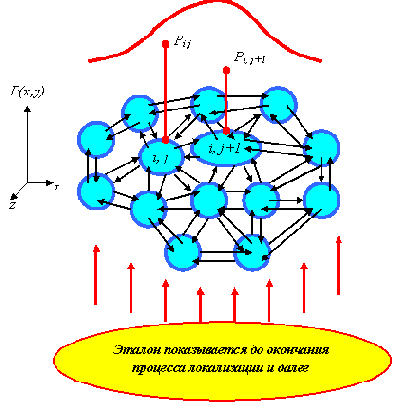
Рис. 2.18. Проблема локализации возбуждения
При подтверждаемом на входном слое эталоне, т.е. при существовании на некотором отрезке времени характера и величины возбуждений, обусловливающих возбуждение выходного слоя, на выходном слое, в частности между нейронами (i, j) и (i, j+1) , происходит перераспределение величины возбуждения.
А именно: несомненно, уменьшится значение Pij
, но в еще большей степени уменьшится значение Pi,j+1
. В следующем такте более "сильный" нейрон еще более "ослабит" более "слабый" нейрон, который, в свою очередь, сможет еще в меньшей степени "ослабить" более "сильный" нейрон и т.д. Более того, "слабый" нейрон может "слабеть" до тех пор, пока взвешенная сумма подаваемых ему сигналов не станет меньше его порога.

Рис. 2.19. Локализация возбуждения
Рассматривая этот процесс в рамках взаимодействия всех нейронов области выходного слоя, можно сделать вывод о постепенной концентрации высокого уровня возбуждения, присущего одному или нескольким нейронам и определяющего один или несколько локальных максимумов.
При таком взаимодействии нейронов области возбуждения выходного слоя происходит лишь усиление сигнала наиболее возбужденного нейрона. Полное подавление возможно лишь на границе этой области. Если где-то внутри области возбуждение некоторого нейрона окажется подавленным полностью (сигнал не преодолевает порога), то в следующем такте этот нейрон не сможет подавить сигнал того нейрона, который до того имел более слабый сигнал возбуждения. Тогда возможно появление в такой области возбуждения нового локального максимума. Таким образом, веса отрицательных связей должны способствовать максимальному усилению возбуждения того нейрона, который первоначально продемонстрировал максимальное возбуждение, при затухании возбуждения нейронов в сторону периферии.
На человеческом языке это означает: "Любое угадывание не исключает сомнений".
Однако всегда ли необходимо на выходном слое локализовать величину возбуждения?
По-видимому, такое усиление уровня возбуждения необходимо для того, чтобы единственный нейрон выходного слоя преодолел некоторую "планку" (изменяющуюся?), чтобы объявить себя ответственным за сделанный вывод или решение.
Однако следует отметить, что локализация и максимизация возбуждения на выходном слое особенно важны тогда, когда действительно необходима высокая степень определенности. Это важно в том случае, если получаемый вывод (решение) немедленно участвует в цепочке последующих, использующих его выводов.
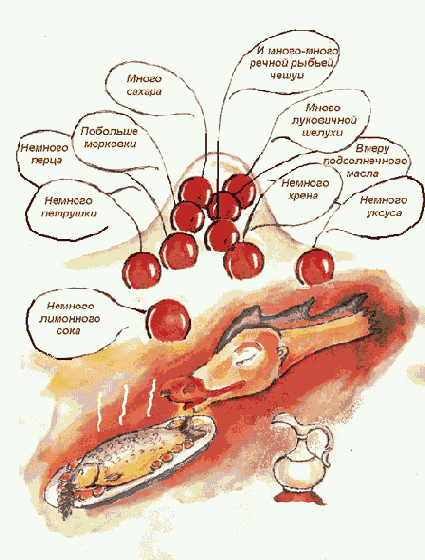
Рис. 2.20. Нейродегустатор
В конце концов, все обусловлено назначением сети, решаемой задачей. Можно представить себе возможный аттракцион - реакцию фантастического чудовища на изображение, как это представлено на
рис. 2.10 и рис. 2.11. По виду изображения инициируются те или иные программы действий: радости, гнева, поднятия лап, виляния хвостом и т.д. Возбуждение определенных нейронов выходного слоя связывается с запуском соответствующих программ. Величина возбуждения может являться основным параметром для этих программ. Программы не исключают друг друга, и в одном такте могут запускаться несколько программ.
Можно представить радостную модель гурмана-дегустатора (рис. 2.20), по аромату блюда определяющего состав использованных ингредиентов и приходящего в восторг или в уныние от представленного букета.
В большинстве частных задач, где нейросеть обучается с помощью "учителя", т.е. на основе действий извне при ее настройке, присутствует элемент принудительного закрепления нейронов выходного слоя за выводами. В процессе последующего обучения преимущественно с помощью весов синапсических связей добиваются адекватной реакции сети.
