опыт - предпосылки обобщения
Объединим множество эталонов, требующих возбуждения одного нейрона выходного слоя, понятием "обобщенный эталон". Например, эталоны А1

















Выберем нейросеть, отражающую, как нам кажется, все особенности, которые необходимо учесть при построении алгоритма трассировки, и, как мы уже начали, возьмем тот же пример, который выглядит теперь следующим образом:
 |
(4.1) |
Мы хотим, задавая обобщенный эталон на входе, например из тех, что приведены выше, экономным путем построить, возможно, пересекающиеся пути возбуждения, ведущие от каждого возбужденного входного нейрона в соответствующий нейрон выходного слоя. Способ должен быть экономным в том смысле, что пути должны быть максимально объединены, совмещены, реализуя стратегию слияния и выхода на общую, единую дорогу, ведущую к заветной цели.
При этом мы строим эвристический алгоритм, который крайне экономно расходует ресурсы сети - ее нейроны и связи, но и так же экономно вводит изменения, развивает сеть, если связей оказывается недостаточно.
Ибо мы видели, с каким трудом удается приспособить "готовую" нейросеть под конкретную задачу. Мы постоянно склонялись к вопросу: "А не лучше ли сразу строить сеть "под задачу", а не наоборот?" Нам кажется, мы нашли диалектический компромисс: беря что-то близкое, подходящее, мы минимально переделываем, словно костюм с жмущим гульфиком, купленный в универсальном магазине. Кроме того, нам очень важно сделать алгоритм доступным широким массам студенческой молодежи, овладевшей основами таинства параллельного программирования!

Рис. 4.1. Нейросеть, подлежащая обучению

Рис. 4.2. Матрица следования с транзитивными связями
Пусть выбранная нейросеть представлена на рис. 4.1, где первоначально заданные связи обозначены тонкими стрелками.
Строим соответствующую матрицу следования S и в ней - транзитивные связи (рис. 4.2). Проверяем, все ли нейроны выходного слоя достижимы из любого нейрона входного слоя. Если нет, считаем, что сеть составлена не корректно.
В данном случае из нейрона В1 не исходит ни одной статической цепочки, заканчивающейся нейроном Вых5. Это следует из того, что в строке, соответствующей нейрону Вых5, нет даже транзитивной связи в столбце, соответствующем нейрону В1. То же касается нейрона В3.
Введем синапсические связи В1


Сформируем статический путь возбуждения {B1, A1, C1, C2, C3, C4, C5}


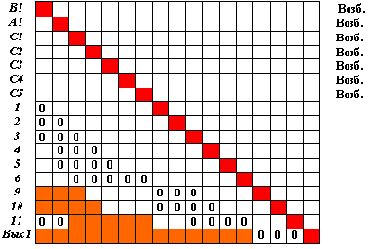
Рис. 4.3. Матрица следования при обучении первому эталону
Пытаясь сымитировать прокладываемые пути возбуждений, снабдим все нейроны входного слоя, отраженные в этой матрице, признаком "возбужден".
Такая строка соответствует нейрону 11. Заменяем в этой строке (в выделенной совокупности столбцов) "нули" "единицами", т.е. максимально увеличиваем веса. Присваиваем нейрону 11 признак "возбужден" и значение m11 = 3. Отражаем изменение весов в матрице S.
Исключаем из матрицы S1 строки и столбцы, соответствующие нейронам В1, А1, 6. Матрица принимает вид, изображенный на рис. 4.5.

Рис. 4.5. Шаг преобразования матрицы следования
Исключаем из матрицы все входы, которые соответствуют нейронам 1, 2, 3, 4, 5, не обладающим признаком "возбужден". Ведь строящийся нами путь возбуждения уже миновал эти нейроны! Исключение этих нейронов породит новые нейроны, нуждающиеся в исключении по той же причине, - нейроны 9 и 10.
Последовательное исключение сверху вниз динамически учитывает появление таких нейронов и гарантирует полное исключение за один проход. Матрица S1 примет вид на рис. 4.6.

Рис. 4.6. Шаг преобразования матрицы следования
Теперь в первом столбце имеется единственная строка с "нулем" - соответствующая нейрону Вых1. Меняем "нуль" на "единицу" - получаем окончательный возможный динамический путь возбуждения по заданному эталону. Изменения отражаем в матрице S.
Мы не будем приводить новый вид матрицы следования S, а на изображении самой сети (рис. 4.7) выделим темным построенную трассу (она же - опорный путь, а также динамический путь возбуждения по предлагаемому эталону).
Реакции на эталон одной комбинации мы сеть научили.
Составим обобщенный эталон ситуации, требующий решения R2, - {A1, B2, B3, C1, C2, C3}. Свяжем это решение с нейроном Вых2.
По сети на рис. 4.7 или по матрице на рис. 4.2 (с учетом частичного обучения!) построим (рис. 4.8) матрицу статического пути возбуждения S2[B2, B3, A1, C1, C2, C3

Нейрон 6 ранее "объединил" возбуждение пяти нейронов: С1, С2, С3, С4, С5, т.е. в матрице S в соответствующей строке содержится пять единиц и m6 = 5. Однако в составленной матрице S2 в строке, соответствующей этому нейрону, присутствуют лишь три единицы.
Значит, этот нейрон не может быть использован для трассировки необходимого пути возбуждения, т.к. комбинация С1&С2&С3&С4&С5 нам здесь не нужна.

Рис. 4.7. Нейросеть, обученная первому эталону

Рис. 4.8. Матрица следования для обучения второму эталону
То же следует сказать и о нейроне 11.
Исключим из данной матрицы строки и столбцы, соответствующие нейронам 6 и 11. Матрица примет вид, показанный на рис. 4.9.

Рис. 4.9. Шаг преобразования матрицы следования
Объединяем столбцы множества входов матрицы, обладающих признаком "возбужден". На данном шаге - это первые шесть столбцов матрицы. Находим в них первую строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 4. Меняем в ней все нули на единицы, полагаем m4 = 4. Присваиваем нейрону 4 признак "возбужден". Отражаем внесенные изменения весов в матрице S.
Исключаем из матрицы S2 строки и столбцы, соответствующие нейронам В2, А1, С1, С2, "передавшим" свое возбуждение нейрону 4.
Вновь объединяем столбцы множества входов, обладающих признаком "возбужден". Это столбцы, соответствующие нейронам В3, С3, 4. В совокупности этих столбцов выбираем первую из строк, содержащую максимальное число нулей. В данном случае это строка, соответствующая нейрону 1. Меняем нуль на единицу, полагаем m1 = 1, нейрону 1 присваиваем признак "возбужден".
Исключаем из матрицы строку и столбец, соответствующие нейрону В3, "передавшему" возбуждение нейрону 1. Исключаем из матрицы строки и столбцы, соответствующие образовавшимся входам - "не возбужденным" нейронам 2 и 3.
Выделяем столбцы, которые соответствуют нейронам - входам, обладающим признаком "возбужден", и в их совокупности находим строку, обладающую наибольшим числом нулей. Такая строка соответствует нейрону 10. Меняем нули на единицы, присваиваем нейрону признак "возбужден", полагаем m10 = 2.
Исключаем из матрицы S2 строки и столбцы, которые соответствуют нейронам 1 и 4, передавшим возбуждение нейрону 10.
Нейрон 9, не обладающий признаком "возбужден", образует вход матрицы. Исключаем соответствующие ему строку и столбец.
Выделяем столбцы, соответствующие нейронам С3 и 10, и в них находим строку с максимальным числом нулей. Первая из таких строк соответствует нейрону 5. Заменяем в ней единственный нуль единицей, присваиваем нейрону признак "возбужден", полагаем m5 = 1. Отражаем изменение веса в матрице S.
Исключаем из матрицы S2 строку и столбец, которые соответствуют нейрону С3, передавшему возбуждение нейрону 5.
Исключаем строку и столбец, соответствующие нейрону 7, как порождающему вход матрицы и не имеющему признака "возбужден".
В совокупности выделенных столбцов, соответствующих нейронам 5 и 10, строка, соответствующая нейрону 12, имеет единственный нуль. Меняем его на единицу, присваиваем нейрону 12 признак "возбужден", полагаем m12 = 1. Отражаем внесенное изменение веса в матрице S. Исключаем из матрицы S1 строку и столбец, соответствующие нейрону 5.
И, наконец, на последнем шаге, заменяя нули в строке, соответствующей нейрону Вых2, единицами, мы получим окончательный искомый путь возбуждения. Отразим его на рис. 4.10 нейросети.

Рис. 4.10. Нейросеть после обучения двум эталонам
Обучим сеть третьей ситуации, требующей решения R3. Закрепим за этим решением нейрон Вых3. Матрица S3[B2, B3, A1, C4, C5


Рис. 4.11. Матрица следования для обучения третьему эталону
Исключаем из матрицы S3 представительство тех ранее использованных ("возбужденных") нейронов, для которых значение m (указано в дополнительном столбце матрицы) превышает количество единиц в соответствующей строке. Это значит, что эти нейроны "собрали" уже возбуждение нейронов, которые в данном пути возбуждения, т.е. в матрице S3, не используются. Это нейроны 4, 5, 6, 11. Переиспользование их невозможно.
Повторяем попытки исключения из матрицы S3 представительства тех нейронов, для которых значение m стало превышать количество единиц в соответствующей строке.
И так далее - до исчерпания этой возможности.
В данном случае нам придется исключить из рассмотрения (вследствие исключения нейронов 4 и 5) нейроны 10 и 12. Матрица S3 примет окончательный вид на рис. 4.12.

Рис. 4.12. Шаг преобразования матрицы следования
Присваиваем всем нейронам, образующим входы матрицы, признак "возбужден".
Выделяем и объединяем столбцы, соответствующие входам матрицы S3.
Разовьем предшествующие аналогичные действия следующим образом.
В выделенных столбцах находим строку, содержащую хотя бы одну единицу. Она (строка) представляет тот нейрон, который "собрал" (при анализе предыдущих эталонов) возбуждение одного или более нейронов, образующих входы. Эти нейроны, "передавшие" свое возбуждение, могут быть исключены из рассмотрения. Среди таких строк выбираем строку с максимальным числом единиц.
Так, нейрон 1 возбужден единственным нейроном, принадлежащим текущему множеству входов матрицы, - нейроном В3. Впредь он представляет этот нейрон, который может быть исключен из рассмотрения. Матрица S3 принимает вид на рис. 4.13.

Рис. 4.13. Шаг преобразования матрицы следования
Подтверждаем нейрону 1 признак "возбужден" и превращаем его во вход матрицы S3, уничтожив веса в его строке.
Вновь находим множество входов матрицы и выделяем соответствующие им столбцы. Пытаемся найти строку, содержащую единицы в этих и только этих столбцах, но таких больше нет. Тогда находим строку, содержащую максимальное число нулей. Первая такая строка соответствует нейрону 2. "Объединяем" на нем возбуждение нейронов В2 и А1, заменяя нули единицами. Полагаем m2 = 2, исключаем нейроны В2 и А1 из рассмотрения, присваиваем нейрону 2 признак "возбужден". Отражаем сделанные изменения весов в матрице S.
Исключаем входы, не обладающие признаком "возбужден", - нейроны 3 и 5.
Выделяем столбцы, соответствующие входам. В их совокупности не находим строк, содержащих единицы. Тогда находим строку, содержащую максимальное число нулей.
Такая строка соответствует нейрону 7. Меняем нули (в выделенной совокупности столбцов!) на единицы, полагаем m7 = 2, присваиваем нейрону 7 признак "возбужден", отражаем изменение весов в матрице S. Исключаем нейроны С4 и С5 из рассмотрения. Сразу замечаем, что сформируется "невозбужденный" вход, соответствующий нейрону 8. Исключаем из рассмотрения и этот нейрон (рис. 4.14).

Рис. 4.14. Шаг преобразования матрицы следования
Выделяем столбцы, соответствующие "возбужденным" входам, и не находим строк, содержащих единицы. Тогда находим первую строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 13. Меняем нуль на единицу, нейрону 13 присваиваем признак "возбужден", полагаем m13 = 1. Исключаем нейрон 7 из рассмотрения.
Выделяем столбцы, соответствующие множеству "возбужденных" входов. В них не находим строку с единицами, но единственная строка с максимальным числом нулей соответствует нейрону Вых3. Меняем нуль на единицу. Однако статус этого нейрона особый, и значение m, как и признак "возбужден", ему не присваиваем.
Исключаем нейрон 13 из рассмотрения.
Выделяем множество столбцов, соответствующих "возбужденным" входам. Это столбцы, соответствующие нейронам 1 и 2. Пытаемся в этих столбцах найти строку с единицами, затем с максимальным числом нулей, - но таковых нет! Значит, необходимо введение дополнительных связей. Тогда в каждом столбце при просмотре сверху вниз находим первую транзитивную связь и меняем ее на единицу. Это означает, что данная сеть дополняется динамическими цепочками возбуждения 1


Построение трассы решения R3 закончено. После этого этапа обучения сеть имеет вид как на рис. 4.15.
Приступим к обучению следующему обобщенному эталону - решению A2&B3&C1&C2&C3&C4&C5


Исключим из рассмотрения те нейроны, для которых количество единиц в строках меньше значения m. Такими нейронами являются 4 и 11. Матрица S4 имеет вид как на рис. 4.17.

Рис. 4.15. Нейросеть после обучения третьему эталону

Рис. 4.16. Матрица следования для обучения четвертому эталону

Рис. 4.17. Шаг преобразования матрицы следования
Присваиваем всем нейронам-входам значение "возбужден". Выделяем столбцы, соответствующие входам - первым строкам "возбужденных" нейронов. Это первые семь столбцов. Среди строк этой совокупности столбцов находим строку с максимальным числом единиц в этих столбцах, при отсутствии единиц в других столбцах. Это строка, соответствующая нейрону 6. Теперь нейрон 6 будет представлять нейроны С1, С2, С3, С4, С5, "передавшие" ему свое возбуждение. Присваиваем ему признак "возбужден", исключаем из рассмотрения перечисленные нейроны, матрица S4 принимает вид как на рис. 4.18.

Рис. 4.18. Шаг преобразования матрицы следования
Для "не возбужденных" нейронов исключаем из матрицы S4 строки (и столбцы), число единиц в которых стало меньше соответствующего значения m. Они соответствуют нейронам 5 и 7. Повторяем этот шаг до полного исключения таких нейронов, - исключаются нейроны 12 и 13. Матрица имеет вид как на рис. 4.19.

Рис. 4.19. Шаг преобразования матрицы следования
Исключаем из рассмотрения множество "невозбужденных" входов. К таким относится нейрон 8. Выделяем множество столбцов, соответствующих входам матрицы. В их совокупности находим первую строку, обладающую максимальным числом нулей (единиц нет во всей матрице!). Такая строка соответствует нейрону 3. Нули в ней соответствуют нейронам В3 и А2. Исключаем эти нейроны из рассмотрения, полагаем m3 = 2, присваиваем нейрону 3 признак "возбужден".
Вновь выделяем множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, находим строку с максимальным количеством нулей. Эта строка соответствует нейрону 14. Заменяем в ней нуль на единицу, полагаем m14 = 1, присваиваем нейрону 14 признак "возбужден".
Исключаем нейрон 6 из матрицы. Матрица принимает вид как на рис. 4.20.

Рис. 4.20. Шаг преобразования матрицы следования
Выделяем множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, находим строку с максимальным количеством нулей. Эта строка соответствует нейрону выходного слоя Вых4. Меняем в ней нуль на единицу. Так как это - нейрон выходного слоя, не присваиваем ему признак "возбужден" и значение m. Исключаем нейрон 14 из рассмотрения. Матрица имеет вид как на рис. 4.21.

Рис. 4.21. Шаг преобразования матрицы следования
В этой матрице множество "возбужденных" входов составляет единственный нейрон 3. Однако в его столбце нет ни единичных, ни нулевых элементов. Тогда, как и прежде, вводим в сеть дополнительную связь, найдя в столбце, соответствующем нейрону 3, первую сверху транзитивную связь и положив ее вес равным единице. Эта связь порождает динамический путь возбуждения 3

Построение трассы решения R4 закончено. Не приводя промежуточного вида матрицы S, дадим на рис. 4.22 вид сети, полученной после данного этапа трассировки.
И, наконец, приступим к трассировке последнего пути возбуждения. Он осуществляется по обобщенному эталону, требующему решения R5, A2&B1&B2&C1&C2&C3&C4&C5

На основе текущего вида матрицы S построим матрицу S5[B1, B2, A2, C1, C2, C3, C4, C5


Рис. 4.22. Нейросеть после обучения четырем эталонам

Рис. 4.23. Матрица следования для обучения пятому эталону
Присваиваем всем входам признак "возбужден".
Выделяем столбцы, соответствующие "возбужденным" входам. В совокупности этих столбцов находим строку, содержащую максимальное число единиц в этих и только этих столбцах, если таковые имеются. В данном случае это строка, соответствующая нейрону 6. Присваиваем нейрону 6 признак "возбужден" и исключаем из рассмотрения нейроны С1, …, С5.
Исключаем из рассмотрения нейроны 5 и 7, так как в соответствующих им строках отсутствуют единицы при отличных от нуля значениях m. Однако видно, что после их исключения придется исключить по той же причине нейроны 12 и 13. Получившаяся матрица представлена на рис. 4.24.

Рис. 4.24. Шаг преобразования матрицы следования
Исключаем из рассмотрения "невозбужденный" вход, соответствующий нейрону 8. Выделяем столбцы, соответствующие "возбужденным" входам, и в их совокупности находим строку, содержащую наибольшее число единиц при отсутствии единиц в других столбцах. Такая строка соответствует нейрону 14. Исключаем из рассмотрения нейрон 6 как передавший свое возбуждение нейрону 14, присваиваем нейрону 14 признак "возбужден". Матрица S5 принимает вид как на рис. 4.25.

Рис. 4.25. Шаг преобразования матрицы следования
Выделяем столбцы входов, соответствующие "возбужденным" нейронам, и в их совокупности находим строку, содержащую максимальное число нулей (строк с единицами больше нет). Такая строка соответствует нейрону выходного слоя Вых5. Меняем нули на единицы. Исключаем нейроны В1 и 14 из рассмотрения. Отражаем введенные изменения в матрице S. Новый вид матрицы S5 приведен на рис. 4.26.

Рис. 4.26. Шаг преобразования матрицы следования
Выделяем множество столбцов, соответствующих входам матрицы. В этих столбцах не находим ни строк, содержащих единицы, ни строк, содержащих нули. Тогда в каждом столбце заносим единицы на места транзитивных связей, то есть вводим связи В2


Трассировка (обучение сети по обобщенным эталонам) закончена. Окончательный ее вид представлен на рис. 4.27, где, напоминаем, веса, принявшие значение 1, соответствуют жирным стрелкам.

Рис. 4.27. Обученная нейросеть
