Динамизм обучения
На самом деле обучение не бывает внезапным, как мы это представили выше, рассматривая сразу обобщенные эталоны. Мгновенное заполнение губки памяти нашего разума из Всеобщего Информационного Пространства в момент рождения - лишь фантастическая мечта, которая опирается на опыт предшествующих земных цивилизаций, известный восточным учениям. Долгий и тернистый путь образования (слово-то какое в русском языке: образование - создание, произведение, построение, - человека!), предполагает многократность и постепенность, изменяемость в совершенствовании и утверждение, трудоголический надрыв и преодоление, победный клич и разочарование.
Итак, можно учить по "чистым" эталонам, объединив их в эталоны обобщенные. Но "ближе к жизни" можно учить по разным "частным" эталонам (то, что мы называем жизненным опытом), приводящим к одному решению. Например, можно (возвращаясь к многострадальному примеру) последовательно "показывать" эталоны B1&A1&C2, B1&A1&C1 и т.д., приводящие к решению R1. Можно предъявлять вперемежку разные эталоны, приводящие к разным решениям. И это справедливо соответствует диалектике познания на основе гипотез, экспериментов и опыта, гласящей, что мир познаваем, но всего познать нельзя, ибо, мы добавляем, - Бесконечность!
Например, дядя Рамзай не мог ранее предвидеть некоторых комбинаций событий, предварительно имея ошибочное суждение о распределении работ своих клиентов. Или ему даже пришлось употребить свои связи для того, чтобы осуществить вожделенную мечту: включить в орбиту своих действий восхитительную многоприбыльную продукцию фирмы Ночная Бабочка!
Во всех случаях на этапе обучения целесообразно определять события А, В, С с максимальной достоверностью, равной единице, рассчитывая тем самым реакцию нейросети на вполне определенные ситуации. Это следует из того, что даже возникшая при предъявлении эталона малая величина возбуждения нейрона входного слоя указывает, что событие возможно и, следовательно, нуждается в рассмотрении.
Интуиция же нам подсказывает, что надо действовать как-то проще, тем более что мы не постесняемся ввести дополнительные связи в сеть, если понадобится.
Итак, рассмотрим проблему динамического включения новых частных эталонов в состав обобщенного эталона на фоне уже произведенного частичного обучения нейросети.
Пусть предъявление эталонов A1&B1&C2 и A1&B1&C4 ("текущий" обобщенный эталон A1&B1&C2&C4), требующих решения R1, а также предъявление текущих обобщенных эталонов A1&B2&C1&C2&C3, A1&B2&C4&C5, A2&B3&C1&C2&C3&C4&C5, A2&B1&C1&C2&C3&C4&C5, требующих соответственно решений R2, R3, R4, R5, привели к трассировке нейросети (к ее текущему состоянию), представленной на рис. 5.1.
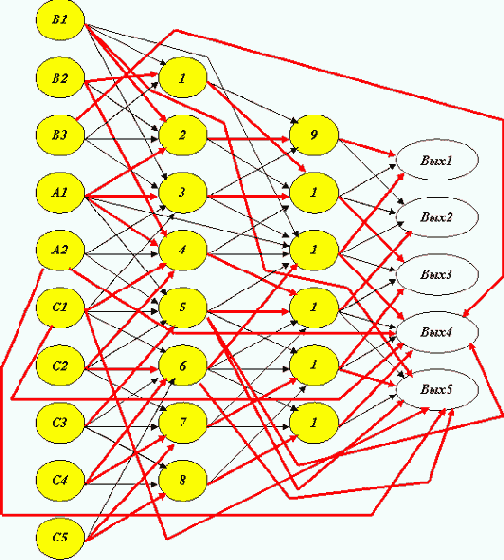
Рис. 5.1. Частично обученная нейронная сеть
Здесь "жирные" связи обладают максимальным значением веса (скорее всего - единичным). Такое состояние получено с помощью алгоритма трассировки, представленного в предыдущей лекции, и это предлагается проверить читателю в порядке закрепления материала.
Матрица следования S, соответствующая получившейся сети, показана на рис. 5.2.
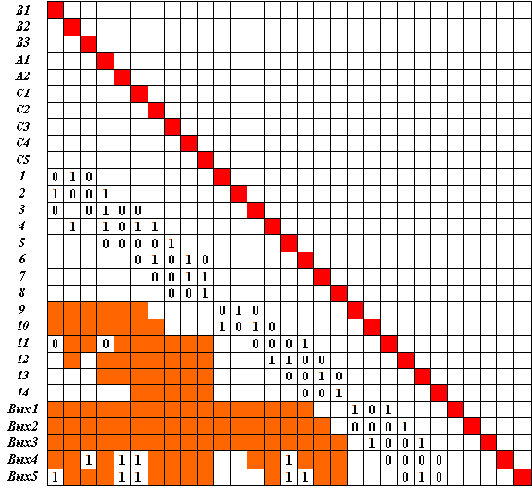
Рис. 5.2. Матрица следования
Как видим, сеть оказалась весьма "запутанной" дополнительными связями. Обучение всем обобщенным эталонам сразу (пример в лекции 4) выявляет термы, использующиеся при получении различных решений. Здесь же термы не складывались, нейроны почти не переиспользовались.
Это и привело к формированию большого числа дополнительных связей. (Мы не любим, когда из нас "вытягивают" одно за другим. Мы возмущаемся: "Не тяни, выкладывай все, что тебе нужно!")
То есть нам необходимо построить путь возбуждения (трассы) B1, A1, C1, C2, C3, C4


Значит, надо проложить трассы, дополнить сеть путем возбуждения C1, C3

Преследуя эту цель, мы не должны допустить слияния, влияния этого пути на пути возбуждения, ведущие в другие нейроны выходного слоя. Такая опасность кроется в естественном желании переиспользования нейронов. Ведь слияние двух путей возбуждения заключается в том, что у некоторых нейронов следует повысить веса синапсических связей (скажем, положить равным единице, вместо нуля, окрасить в красный цвет). То есть некоторые нейроны могут стать преемниками возбуждения большего, чем прежде, числа нейронов. А если эти нейроны использовались для получения других решений?
Здесь важно сделать Замечание в дополнение к алгоритму трассировки, рассмотренному в лекции 4:
целесообразно при переиспользовании нейронов, возникающем при последовательном анализе обобщенных эталонов , фиксировать информацию: участвует ли данный нейрон лишь в одном пути возбуждения - к единственному нейрону выходного слоя и к какому именно, или к более чем к одному нейрону выходного слоя. И этого будет вполне достаточно для ликвидации тревог.
Продолжим рассмотрение примера, ведущее к обобщению.
Для нового обобщенного эталона на основе матрицы S, так же, как мы это делали в предыдущем разделе, построим (рис. 5.3) матрицу S*[B1, A1, C1, C2, C3, C4

В соответствии с правилом ее построения в ней представлены лишь те нейроны, для которых число единиц в строке равно соответствующему значению m. Для каждой строки, содержащей единичные элементы, указано, используется ли нейрон для получения единственного решения и какого (признак Выхi), или не единственного (признак отсутствует).

Рис. 5.3. Матрица следования для обучения уточненному эталону
Исключим из построенной матрицы строки и столбцы, соответствующие нейронам, участвующим в путях возбуждения, не ведущих в Вых1 (рис. 5.4). (В общем случае в матрице могли сохраниться строки, содержащие нулевые веса.)

Рис. 5.4. Шаг преобразования матрицы следования
"Спускаемся" по столбцу, соответствующему нейрону С1, и в строке, не являющейся входом, находим, если таковой имеется, первый нулевой элемент. Полагаем его равным единице и отражаем введенное изменение в матрице S. Если нулевого элемента в столбце не нашлось, находим первый "пустой" элемент (или отмеченный транзитивной связью - все равно) и полагаем его равным единице. Этим мы вводим дополнительную связь, отраженную в матрице S. В данном случае такой связью с единичным весом является связь С1

То же проделываем с нейроном С3, введя дополнительную связь с единичным весом С3


Рис. 5.5. Шаг преобразования матрицы следования
Отметим, что наше решение основано на эвристике, и место появления новых возбужденных связей может быть оспорено. Например, могли быть построены связи С1






Мы не приводим еще более усложнившегося рис. 5.1 уточненной сети, предоставив читателю возможность проверить усвоение материала с помощью легкого нажатия красным карандашом прямо в книжке в направлении стрелок, которые исходят из кружочков, помеченных символами С1 и С3, и входят в кружок, помеченный цифрой 2. Однако намек на такое уточнение делаем на рис. 5.6.

Рис. 5.6. Полностью обученная нейросеть (намек)
